Timings and experimental set-up

All timings in this study were done on a collection of six machines, using clang as the compiler, and testing on a set of 17 matrices chosen from the Matrix Market. Times for matrix multiplication are obtained by doing 10,000 multiplications, repeating that five times, and selecting the minimum of those five times. The machines and matrices are described on this page, and our decision to use minimum times (rather than median) is discussed. The files containing timings are at the bottom of this page.

Machines

Six computers were used to produce timings for each of the “Specializers” developed in this study. The main characteristics of these computers are described below. The information was obtained from each computer's /proc/cpuinfo and /proc/meminfo files.

Computer	Processor	cpu (MHz)	CPU cache size (Kb)	MemTotal (Kb)	OS
loome1	Intel(R) Xeon(R) CPU E5640 @ 2.67Ghz	2660.081	12288	12291944	Linux CentOS release 5.8
loome2	Intel(R) Core(TM) i7 CPU 880 @ 3.07GHz	1200.000	8192	8132912	Linux CentOS release 5.8
loome3	Intel(R) Core(TM) i5-2400 CPU @ 3.10GHz	1600.000	6144	8063880	Linux CentOS release 5.8
i2pc4	Intel(R) Xeon(R) CPU L7555 @ 1.87GHz	1861.989	24576	65955912	Scientific Linux release 6.3
chicago	Intel(R) Core(TM)2 Duo CPU P8600 @ 2.40GHz	2400.000	3072	2097152	MacOS Lion 10.7.4
pl	Intel(R) Xeon(R) CPU E5405 @ 2.00GHz	1994.768	6144	2057296	Ubuntu Linux 10.04 LTS

Matrices

A set of 17 matrices were selected to conduct the test on the specializers. The matrices were obtained from the Matrix Market site (http://math.nist.gov/MatrixMarket/). The main characteristics of the matrices are summarized below. All information and images are from the Matrix Market, except for the non-zero counts; the Matrix Market representation (mtx) sometimes includes zeros (we don't know why), but we are reporting only actual non-zeros.

Name	Size	Non-zeros
add32	4960x4960	19848
cavity02	317X317	5923
cavity23	4562X4562	131735
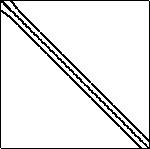
fidap001	216X216	4339
fidap005	27X27	279
fidap031	3909	91165
fidap037	3565X3565	67591
memplus	17758X17758	99147
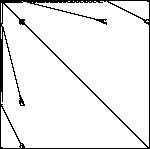
mhd3200a	3200X3200	68026
mhd4800a	4800X4800	102252
nnc666	666X666	4032
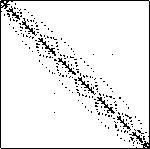
orsreg_1	2205X2205	14133
pde900	900X900	4380
rdb2048	2048X2048	12032
saylr4	3564X3564	22316
sherman5	3312X3312	20793
utm5940	5940X5940	83842

Selecting Representative Time for the Specializers - Min Vs Median

Specializers are compared based on the time they spent to solve a given matrix. It is important to report the right time for a given specializer, which is not as simple as it sounds: as is well known, timings for the exact same computation, on the same machine, with the same inputs, can vary "randomly." The approach we used was to run each generated program five times (10,000 multiplications each time) and select the most representative time. However, which out of the five times can be considered the most representative of the set? Two answers were considered for this question: the minimum time and the median time. We use the minimum, for reason we now explain.

Although the median is more often used in statistical reports, we would argue that in this case, as a matter of principle, the minimum time is more meaningful. A computer can perform a given computation in some minimal amount of time; if it takes more time, it is because some event not associated with the computation slowed it down; our goal is to get the "cleanest" timing we can, so we would prefer the one that is contaminated by the fewest external events; that would be the minimum.

But there is another issue, and it is why median is used more often in other types of statistics, which is the issue of reproducibility, or predictability. In many situations, in a given set of samples, the extremes are considered more likely to be anomalous and to result from some random and unpredictable event. Thus, it is common to discount the highest and lowest measurements; taking the median is one way to do that. However, the argument made in the previous paragraph suggests that that might not be the case for the kinds of measurements we are taking. The question here is one of, so to say, expedience: which approach gives us the "smoothest" results, i.e. the results less likely to vary wildly and unpredictably.

One way to ask this question is just this: If we perform our experiment in the way outlined above - five runs of 10,000 multiplications - on the same code multiple times, which method will produce results that are more similar across those trials: minimum or median?

To settle this question, seven specializers and three matrices were randomly selected. Programs were generated for each specializer-matrix combination. Each generated program was used to produce twenty sets of five timing results; that is, we ran our usual method twenty times. Then the coefficient of variation of 20 minimum times was compared with the coefficient of variation of 20 median times. The tests were conducted on four computers: loome1, loome2, loome3, and i2pc4.

The coefficient of variation is a normalized measure of dispersion of a probability distribution, defined as the ratio of the standard deviation to the average of the sample.

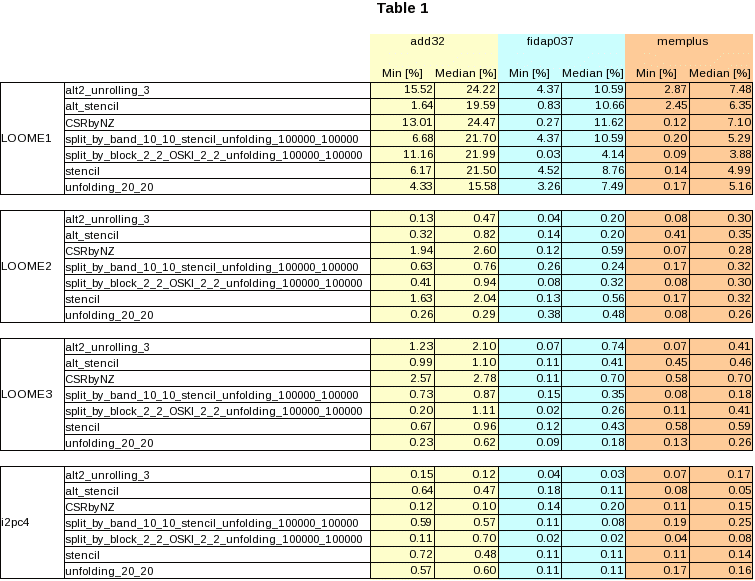
Table 1 shows the coefficient of variation of minimum and median time values for each of the selected specializers and matrices over the four computers used for the tests.

Analyzing the results shown on Table 1 we can state the following observations:

On all machines except loome1, the coefficients of variation are small: always less than 3%, almost always less than 1%. That is, the timings were quite uniform, so that the choice of median or minimum would not make much difference in either case.

Loome1 is the most unpredictable machine. On this machine, the minimum produced less variation among the twenty runs in every case, often dramatically less.

On loome2 and loome3, minimum produced less variation than median in 41 out of 42 trials.

Only on i2pc4 was median competitive with minimum on the measure of low variance, taking the prize ten times (compared to eight for minimum, with three ties). However, i2pc4 is, in general, our most predictable machine; the coefficients of variation of minimum and median times are so small - less than 1% for all cases - that it would appear the choice simply does not matter.

The above discussion leads us to the conclusion that the minimum time value obtained from a set of runs of a given test (specializer-matrix-computer) is the most appropriate time to report. Thus, all timings we give on our web pages and papers (including the ones just below) are obtained by the method described in the first paragraph of this page.

CSV files

We will add CSV files as we do more experiments. For now, we have only the timings for the basic methods. (We have many, many more timings, of course, but mostly they don't seem very meaningful.) The format of each file is a series of lines of the form: machine, matrix, method, time (microseconds for 10,000 calls to multByM).

CSV file containing timings of all basic methods on all (seven) machines. These are:
- CSRbyNZ.
- OSKI_1_2, 2_1, and 2_2. Technically, this is a mixed method: if the blocks don't fit exactly, there are leftover elements in the bottom row and/or far right column. These are handled by unfolding.
- CSR_1, ..., CSR_10.
- Unfolding. In terms of the specialize.py generator, this is "unfolding, 1000000, 1000000", i.e. this is unfolding with exactly one assignment per row.
- stencil.
- diagonal. Again, this is a mixed method. In terms of specialize.py, this is obtained with argument [split_by_dense_band, 1000000, 1000000, 80, [diagonal], [unrolling, 2]]. That is, every diagonal that is at least 80% dense is handled by diagonal, and the rest are handled by CSR_2. Note that do not have timings for loome1 for this method.
- MKL. Again, we do not have timings for loome1 for this method.

Last updated on Mon Aug 13 10:22:31 CDT 2012